What Einstein said of Mahatma Gandhi, that generations to come will scarcely believe that such a one as this ever, in flesh and blood, walked upon this earth, is more than applicable to Einstein himself. From 2005 – declared by the United Nations as the World Year of Physics, to celebrate the centenary of Einstein’s annus mirabilis – onward, there have been many occasions to mark one hundred years of one or the other incredible contribution of his. For Einstein, many years were very good indeed.
What makes 1917 special in some ways is the appearance of three other papers, each unrelated to the other (as the three of 1905) and which altered the fields that they touched upon. It would well have been called another annus mirabilis, had not 1905 already happened.
Early on in Volume 6 of the Collected Papers of Albert Einstein titled The Berlin Years: Writings, 1914-1917, his “Inaugural Lecture”, delivered upon his election to the Prussian Academy of Sciences, he alludes to the soon-to-be-presented papers on his General Theory of Relativity, saying “We have determined that inductive physics has questions for deductive physics and vice versa; and eliciting the answers will require the application of our utmost efforts. May we, by means of united efforts, soon succeed in advancing toward conclusive progress.” That conclusive progress was to appear in the journal Annalen der Physik in May 1916, entitled “Die Grundlage der Relativitätstheorie” (On the Theory of General Relativity). But that was 1916.
The first of 1917’s three gems was On the Quantum Theory of Radiation, wherein he came up with stimulated emission and laid the foundations of laser physics. The second was Cosmological Considerations in the General Theory of Relativity, in which he set the foundations of modern cosmology.
And the third. On May 11, 1917, Einstein presented a paper to the German Physical Society, and this was published on the 30th of the same month, in the journal Deutsche Physikalische Gesellschaft. Verhandlungen, 19, 82-92 (1917). Titled On the Quantum Theorem of Sommerfeld and Epstein, this paper essentially anticipated Hamiltonian chaos and its implications for quantum mechanics, the field of Quantum Chaos. Considering that it was written before wave mechanics and the Schrödinger equation, this paper is remarkable, also because Einstein seems to have explicitly understood the quantum implications of classical nonintegrability.
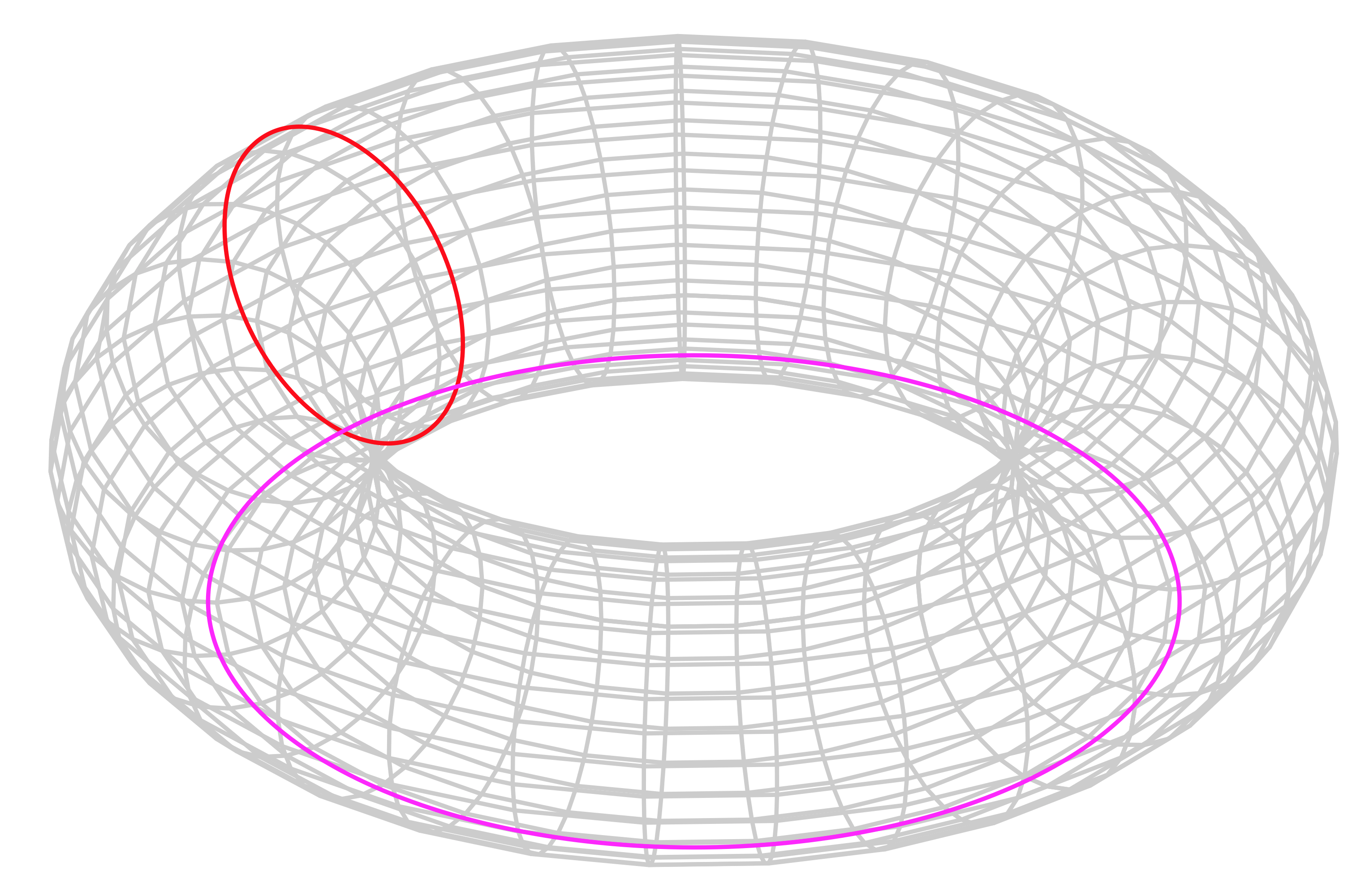
As he puts it, if one examines any volume element in configuration space, any given orbit can pass through that region infinitely many times, either (a) with a (few) well defined values of the momentum – as on a torus – or (b) “there are infinitely many [values of the momentum] at the location under consideration“. In other words, small changes in the positions can correspond to very different momenta. Another way of saying something similar had to wait for Ed Lorenz in the 1960’s, who termed this as sensitive dependence on initial conditions, or what we term today as classical chaos.
The quantum condition he derives (and which now goes by the name of Einstein-Brilloiun-Keller-Maslov or EBKM quantization) uses the classical invariants identified by Poincaré, and Einstein goes on to give, in his view, the proper quantum conditions (11) that correspond to integrals along independent paths on n-dimensional tori (as in the figure above).
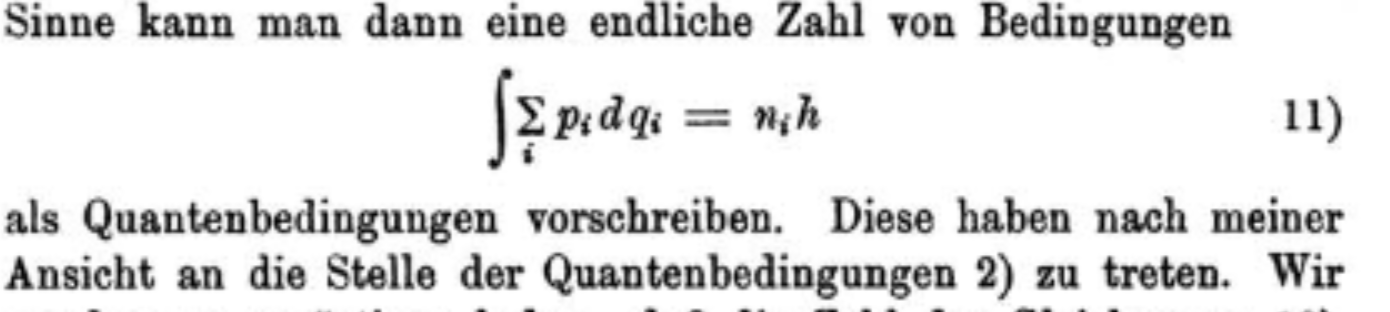
But being Einstein, he “notices immediately that type b) excludes the quantum condition we formulated” earlier in the paper: this is the insight that was to lead half a century later, to the beginnings of the field of quantum chaos, the knowledge that there were classical motions for which quantum conditions could be stated, and those for which it was not possible, at least not in the same way. More can be read about “Einstein’s Unknown Insight and the Problem of Quantizing Chaos” in Douglas Stone’s article in Physics Today in 2005.
I first came across this paper of Einstein’s in 1978 or 1979 as a postdoc when I was struggling through Arnold’s text on Classical Mechanics and working on semiclassical mechanics. It may (OK, does) not count among Einstein’s greatest works, but arguably it is the one that has had the greatest impact on my own research. Other works of Einstein have had a much bigger impact on all our lives, of course, but this one is a paper whose centenary I’d like to mark.
And the other two as well. 2017 is the centenary of another annus mirabilis, a smaller one than 2005 perhaps, but enormous by any other standards.